古诺模型 -亚博电竞网

　　古诺模型也被称为“双头模型”，是早期的寡头模型。它是由法国经济学家古诺于1838年提出的。古诺模型是一个只有两个寡头厂商的简单模型，其结论可以很容易地推广到三个或三个以上的寡头厂商的情况中去。

　　古诺模型假设市场上只有a、b两个厂商生产和销售同一种成本为零的产品，两个厂商都准确地了解市场的需求曲线，他们在已知对方产量的情况下，各自确定能够给自己带来最大利润的产量，在这样的假设下，a、b的均衡产量都等于市场需求量的1/3，整个行业的均衡产量等于市场需求量的2/3。将该模型的结论推广到m个厂商，则每个厂商的均衡产量为市场最大需求量的1/m 1，总产量则为市场最大需求量的m/m 1。

　　假定：市场上只有a、b两个厂商生产和销售相同的产品，它们的生产成本为零；它们共同面临的市场的需求曲线是线性的，a、b两个厂商都准确地了解市场的需求曲线；a、b两个厂商都是在已知对方产量的情况下，各自确定能够给自己带来最大利润的产量，即每一个厂商都是消极地以自己的产量去适应对方已确定的产量。

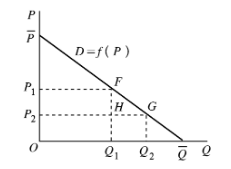
　　当生产成本为零，寡头厂商数量为，结论为：

　　每个寡头厂商的均衡产量=市场总容量

　　行业的均衡总产量=市场总容量

　　假设有两个寡头垄断厂商的行为遵循古诺模型，他们的成本函数分别为：tc1=0.1q1^2 20q1 100000，tc2=0.4q2^2 32q1 20000。这两个厂商生产一同质商品，其市场需求函数为：q=4000-10p。根据古诺模型，试求：

　　（1）厂商1和厂商2的反应函数；

　　（2）均衡价格和厂商1级厂商2的均衡产量。

　　解答：

　　(1）为求厂商1和厂商2的反应函数，先要求二厂商的利润函数。由已知市场需求函数，可得p=400一0.1q，而市场总需求量为厂商1和厂商2产品需求量之和，即q=q1十q2，因此，p=400-0.1q=400-0.1q1-0.1q2。由于两个厂商生产一同质商品，从而可知其市场价格相等，即p1=p2=p。由此求得两厂商的总收益函数分别为

　　tr1=p*q1=400q1-0.1q1^2--0.1q1*q2

　　tr2=p*q2=400q2-0.1q2^2-0.1q1*q2

　　于是，两厂商的利润函数分别为

　　π1=tr1-tc1=400q1-0.1q1^2-0.1q1*q2-0.1q1^2-20q1-100000

　　π2=tr2-tc2=400q2-0.1q2^2-0.1q1*q2-0.4q2^2-32q2-20000

　　两厂商要实现利润最大，其必要条件是：

　　απ1/αq1=400-0.4q1-0.1q2-20=0

　　由此得q1=950-0.25q2，该式即为厂商1的反应函数。

　　同理可得厂商2的反应函数为q2=368-0.1q1

　　(2）均衡产量和均衡价格可以从上述反应函数(曲线）的交点求得。为此，可将上述两个反应函数联立求解：

　　q1=950-0.25q2

　　q2=368-0.1q1

　　得q1=880，q2=280，q=880 280=1160,p=400-0.1q=284